Boolean Algrebra

Boolean algebra is different from elementary algebra as the latter deals with numerical operations and the former deals with logical operations. Elementary algebra is expressed using basic mathematical functions, such as addition, subtraction, multiplication, and division, whereas Boolean algebra deals with conjunction, disjunction, and negation. In binary 1 = true and 0 = false.

Operations

Operations of boolean algebra are:

  • AND operation (denoted A⋅B)
  • OR operation (denoted A+B)
  • NOT operation (denoted A’)

AND

Boolean multiplication corresponds to the logical function of an “AND” gate, as well as to series switch contacts:

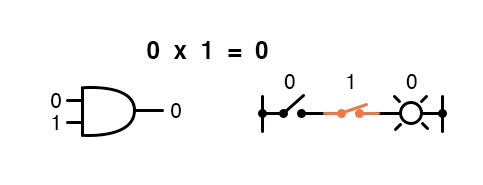
OR

Boolean addition corresponds to the logical function of an “OR” gate, as well as to parallel switch contacts:

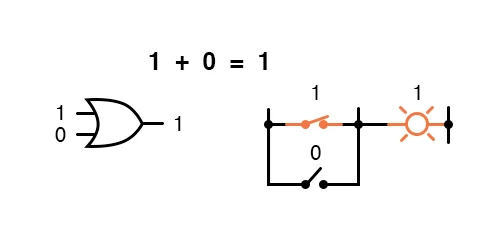
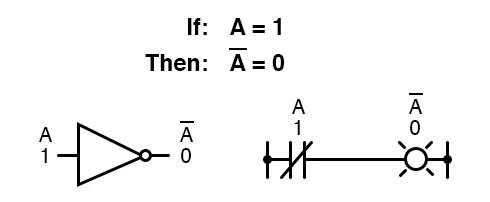
NOT

Boolean complementation finds equivalency in the form of the NOT gate, or a normally-closed switch or relay contact:

Logic Operations

NOT AND OR
0’ = 1 0 ⋅ 0 = 0 0 + 0 = 0
1’ = 0 0 ⋅ 1 = 0 0 + 1 = 1
  1 ⋅ 0 = 0 1 + 0 = 1
  1 ⋅ 1 = 1 1 + 1 = 1

Properties of Boolean Algebra

Annulment law – a variable ANDed with 0 gives 0, while a variable ORed with 1 gives 1, i.e.,

A ⋅ 0 = 0 
A + 1 = 1

Identity law – in this law variable remain unchanged it is ORed with ‘0’ or ANDed with ‘1’, i.e.,

A ⋅ 1 = A 
A + 0 = A

Idempotent law – a variable remains unchanged when it is ORed or ANDed with itself, i.e.,

A + A = A 
A ⋅ A = A

Complement law – in this Law if a complement is added to a variable it gives one, if a variable is multiplied with its complement it results in ‘0’, i.e.,

A + A' = 1 
A ⋅ A' = 0

Double negation law – a variable with two negations, its symbol gets cancelled out and original variable is obtained, i.e.,

((A)')'=A

Commutative law – a variable order does not matter in this law, i.e.,

A + B = B + A 
A ⋅ B = B ⋅ A

Associative law – the order of operation does not matter if the priority of variables are the same like ‘*’ and ‘/’, i.e.,

A+(B+C) = (A+B)+C 
A ⋅ (B ⋅ C) = (A ⋅ B) ⋅ C

Distributive law – this law governs the opening up of brackets, i.e.,

A ⋅ (B+C) = (A ⋅ B)+(A ⋅ C) 
(A+B)(A+C) = A + BC

Absorption law –:-This law involved absorbing similar variables, i.e.,

A ⋅ (A+B) = A 
A + AB = A 
A+ A'B = A+B 
A(A' + B) = AB

De Morgan law – the operation of an AND or OR logic circuit is unchanged if all inputs are inverted, the operator is changed from AND to OR, and the output is inverted, i.e.,

(A ⋅ B)' = A' + B' 
(A+B)' = A' ⋅ B'

Hacks

  • Explain in your own words the functionality of each property of boolean algebra on your own blog
  • explain the significance of logic gates in modern computing and how boolean algebra relates to it